Update! Paper published in a scientific journal: doi.org/10.3390/axioms13050323.
As the leaves begin to fall and the warmth of summer ends, so too does my journey with Google Summer of Code (GSoC) this year. Since June, I've been actively contributing to the Machine Learning for Science (ML4SCI) open-source organization. My work has revolved around exploring how to adapt the vision transformer (ViT) so that it is executed on quantum computers, that is, on how to develop a quantum vision transformer (QViT). In particular, the focus has also been on applying the models to high-energy physics (HEP) data produced by the Large Hadron Collider (LHC) at CERN.
In this comprehensive blog post, I start by explaining my experience on GSoC and, in particular, how it has been as a contributor to ML4SCI. Next, I dip into a brief introduction to quantum machine learning. Then, I dive into the specifics of my project, explaining the experiments I've carried out, illustrating the proposed model, and presenting the results obtained. Lastly, I also lay out some possible future directions and give some final thoughts and acknowledgements. All the code for the project is available in the salcc/QuantumTransformers repository (as well as in in the ML4SCI/QMLHEP repository).
My experience in Google Summer of Code with ML4SCI
Google Summer of Code (GSoC) is a global online program run by Google with the aim of bringing new contributors to open-source projects. Many open-source organizations propose various projects during the spring. Then potential contributors can apply for each project, and the organizations pick the ones they think are the best fit. The selected contributors are then paid a stipend by Google to work on the project during the summer. Google doesn't play a big role in how organizations and contributors work together. However, they do an excellent work organizing the program, providing the platform to list projects and apply to them, keeping track of the progress of the contributors, and also quite importantly, paying them.
I discovered GSoC in high school because I was quite interested in free and open-source software development. Nonetheless, you have to be at least 18 to join, which was not my case at the time. However, another program called Google Code-in (GCI) existed, which was similar to GSoC, but for pre-university students. Instead of big projects that span the whole summer, participants completed multiple smaller tasks to contribute to open-source projects as well. At the end of the program, each open-source organization selected two Grand Prize Winners, who were given a trip to visit San Francisco and the Googleplex HQ in Mountain View. I took part in 2018 contributing to the RTEMS Project, and I was one of the Grand Prize Winners! It was an amazing experience. Sadly, the GCI program has since been discontinued.
Project selection
Ever since my experience with Google Code-in, I had my sights set on Google Summer of Code. But I wanted to give myself a few years of university first to deepen my knowledge of software development and also artificial intelligence, since I wanted to contribute in some project related to it. By last summer, I felt ready. Excited to participate, I began to explore which organizations seemed interesting to me.
While I enjoy coding and the spirit of open-source, my interest in machine learning and academic research was a driving factor in my search. There are many organizations participating in GSoC, so I feel that there's one (or several) for everyone.
After narrowing down my list of potential organizations, I still had several contenders. It is possible to submit up to three proposals, but making a proposal takes quite a lot of time, and as the applications are during the spring, I still had a lot of work from my university commitments. After exploring the projects of each of these organizations, ML4SCI especially caught my attention as they had projects about quantum machine learning (QML). In particular, ML4SCI has a set of projects that apply QML to high-energy physics (HEP) data, termed QMLHEP for short.
I came across QML during my university studies while learning about support vector machines, which can benefit from being executed on quantum computers. The term alone of quantum machine learning, coupled with the potential I imagined it held, made my curiosity for the field grow. Furthermore, I also wanted to learn about it to be prepared for the future, when quantum computers will surely be more widespread. When I was younger, I had the opportunity to learn a bit about quantum computing, so I already had some background on the fundamentals used. However, I had never had the occasion to learn about QML specifically, let alone get my hands on a related project. So, of course, ML4SCI seemed like the perfect option to both satisfy my curiosity and dive into hands-on work with QML.
Application to ML4SCI
Apart from requiring the proposal, ML4SCI additionally asks applicants to solve some tasks related to the application of deep learning to high-energy physics and quantum machine learning. This could include implementing a (classical) graph neural network to classify between quark and gluon jets, or a quantum generative adversarial neural network.
Out of all the QMLHEP projects ML4SCI put forth, I was drawn to the one focused on quantum vision transformers, as I already had a lot of experience working with transformers, and I had some ideas to make them quantum. After sending in my application, I anxiously awaited the decision. To my excitement, I was selected! For context, this year, ML4SCI saw over 200 applications, of which 23 were accepted for this GSoC 2023.
Community bonding period
After this, I was officially a GSoC contributor, but I still had to do all the work! The first weeks of GSoC are termed the "community bonding period". During this phase, I met the mentors I would have for the rest of the program, as well as my fellow contributors. In particular, I had the pleasure to be guided by Sergei Gleyzer, KC Kong, Konstantin Matchev, Katia Matcheva, Rui Zhang, and Amey Bhatuste. The other contributors of the QMLHEP group this year have been Tom Magorsch (on quantum generative adversarial networks), Roy Forestano and Gopal Ramesh (both on quantum graph neural networks), Cosmos Dong (on quantum equivariant neural networks), and Eyup Unlu (on quantum vision transformers as me). The contributors working on the same topics tried to explore them in different ways.
Since the beginning of the community bonding period, we've been having a weekly Zoom call where we discuss our progress, share ideas and get advice from each other about our projects. We also communicate by chat through Mattermost, which is an open-source clone of Slack developed by CERN. I found our communication channels not only effective and informative, but also a source of motivation, especially during challenging phases. Additionally, we had three broader organization meetings where I was able to meet the other contributors working with ML4SCI and get to know what their projects were about.
And after the community bonding period, the real work begins!
But wait, what's quantum machine learning?
Machine learning revolves around the development of statistical algorithms to model data. The aim is to learn patterns, make predictions, classify and detect objects, or generate new data. For example, converting speech to text, clustering similar customers, recognizing faces, predicting the weather or the risk for disease, distinguishing different images of animals, generating text (like ChatGPT), images (like DALL·E), and much more.
Quantum machine learning (QML) has the same objectives, but the aim is to develop statistical algorithms that leverage quantum computers with the aim of surpassing the "classical" ones, that is, the algorithms that are executed on non-quantum (classical) computers. This aspiration comes from observing that quantum algorithms exist that are much superior than classical ones for some tasks, such as factoring integers (Shor's algorithm) or searching in an unsorted list (Grover's algorithm). QML also has the potential to obtain greater accuracies thanks to the unique properties of quantum circuits, such as access to the exponentially large Hilbert space.
Some examples of QML algorithms are quantum support vector machines, quantum nearest-neighbor algorithms, quantum nearest centroid classifiers, or quantum artificial neural networks. At ML4SCI, we mostly focus on the last case, that is, quantum deep learning. The idea here is to use quantum circuits in which some gates are parametrized and the values of these parameters are learned, like in classical neural networks. Depending on the type of gate used, the values represent different physical parameters, such as the rotation angles of the qubits, electromagnetic field strength, or laser pulse frequency. Moreover, before being able to work with the data in the quantum circuits, we have to encode it into its physical state. Furthermore, upon concluding the circuit's operations, we have to take measurements to extract the final state. Such parametrized quantum circuits are also referred to as variational quantum circuits, or VQCs for short.
Note that typically, as not many quantum computers exist, and they are still in its infancy, the quantum circuits are numerically simulated on classical computers. However, the goal is to be able to execute them on real quantum computers in the future.
The relevance of quantum machine learning and the work of ML4SCI on its application in high-energy physics is accentuated by the upcoming start of operation of the High Luminosity Large Hadron Collider (HL-LHC) at the end of this decade. The program will produce enormous quantities of data, which in turn will require vast computing resources. Consequently, QML emerges as a plausible direction to explore to deal with such huge amounts of data.
Learning more
During my participation at GSoC, some people contacted me to ask how I learned about quantum machine learning and machine learning in general, so I decided to include some pointers here too.
Personally, I learned about machine learning and deep learning at the university. If you are from Catalonia and are interested in artificial intelligence and data science, I strongly recommend the Bachelor's in Data Science and Engineering at UPC (the one I'm pursuing right now). However, I guess most university courses on machine learning will also be good at teaching it. Nonetheless, if you cannot go to a university or are unable to take courses on deep learning, I'd suggest reading Dive into Deep Learning. The explanations are very good, and it's updated, interactive, and free! I also recommend learning PyTorch, as it's the most widely used framework and, in my opinion, the easiest and most understandable one.
On the other hand, universities currently don't typically teach about QML, at least at the undergraduate level. Nevertheless, there are many resources online that are helpful too. I found the PennyLane (a framework for quantum machine learning) tutorials and documentation very helpful to get into QML and refresh quantum computing. PennyLane itself is also a nice framework to get started with QML, although I found out during the project that TensorCircuit is much faster (more on this later).
If you want to get a more comprehensive overview of the of quantum artificial neural networks, I recommend reading the overview "Quantum computing models for artificial neural networks" (2021) by Mangini et al. Finally, if you want to learn about quantum computing, I suggest reading the book "Quantum Computing: An Applied Approach" (2nd Edition, 2021) by Jack D. Hidary, and if you want to go more in depth into the theoretical concepts behind quantum computing and quantum information theory, I recommend reading "Quantum Computation and Quantum Information" (10th Anniversary Edition, 2010) by Michael A. Nielsen and Isaac L. Chuang (sometimes referred as Mike and Ike).
My work on quantum transformers
As mentioned in the beginning, the main focus of my project has been on developing, training, and evaluating quantum vision transformers (QViTs) on high-energy physics data produced by CERN.
The Transformer architecture introduced by Vaswani et al. in 2017 has been a revolutionary development in deep learning, leading to significant advancements in various fields, particularly in natural language processing (for example, the T in the powerful GPT models stands for "Transformer"). Inspired by the success of transformers, more recent work by Dosovitskiy et al. in 2020 also introduced the Vision Transformer, which adapts the original Transformer architecture to handle images by dividing them into non-overlapping patches and processing them using self-attention, that is, they only use the encoder part of the Transformer.
During the project, the spotlight has been primarily on Vision Transformers, as the high-energy physics data in which ML4SCI is interested is mostly in the form of images. However, I also explored the application of the proposed architectures to text just to test the flexibility of the proposed architectures.
Datasets
I mainly worked with four datasets, which I describe next.
MNIST Digits
I used the MNIST Digits dataset for fast prototyping and debugging. This well-known dataset contains 70,000 1-channel 28x28 images of handwritten digits, which are labeled with the corresponding digit. The dataset is split into 60,000 images for training and 10,000 images for testing.
A random example of each digit is shown below:
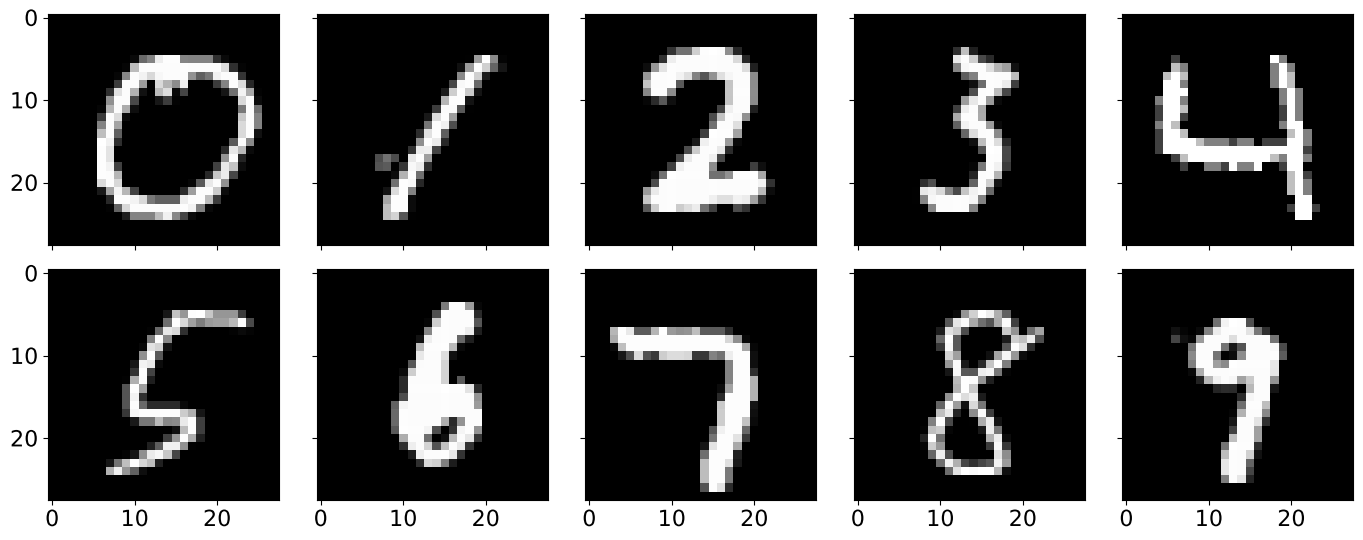
Quark-Gluon
The Quark-Gluon dataset is one of the two main datasets I've been working with. The data is derived by Andrews et al. from simulated data available on the CERN CMS Open Data Portal.
The goal is to discriminate between quark-initiated and gluon-initiated jets. Such task has broad applicability to searches and measurements at the LHC. Consequently, how to solve this task has already been extensively examined with classical machine learning techniques.
The dataset consists of 933,206 3-channel 125x125 images, with half representing quarks and the other half gluons. Each of the three channels in the images corresponds to a specific component of the Compact Muon Solenoid (CMS) detector of the LHC: the inner tracking system (Tracks) that identifies charged particle tracks, the electromagnetic calorimeter (ECAL) that captures energy deposits from electromagnetic particles, and the hadronic calorimeter (HCAL) which detects energy deposits from hadrons.
The following figure shows a random example of jets for both quark (top) and gluon (bottom):
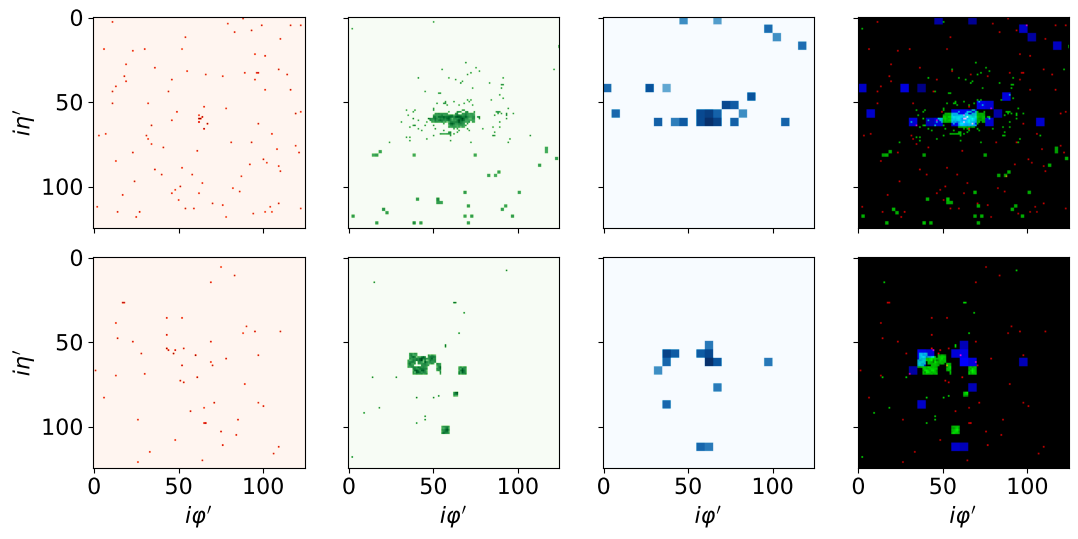
The columns show the distinct sub-detectors: Tracks, ECAL, HCAL, and a composite image combining all three. All images are shown in log-scale and normalized. Note that the ECAL and HCAL were upscaled to match the Tracks resolution.
The following figure shows the average images of quarks (top) and gluons (bottom) across the entire dataset:
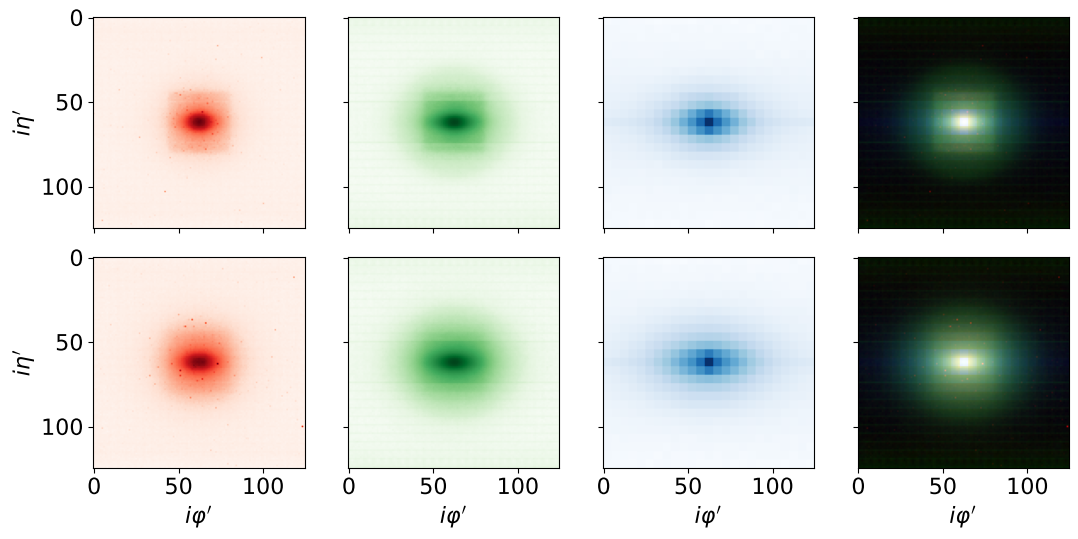
Note the more dispersed nature of the gluon jets across channels.
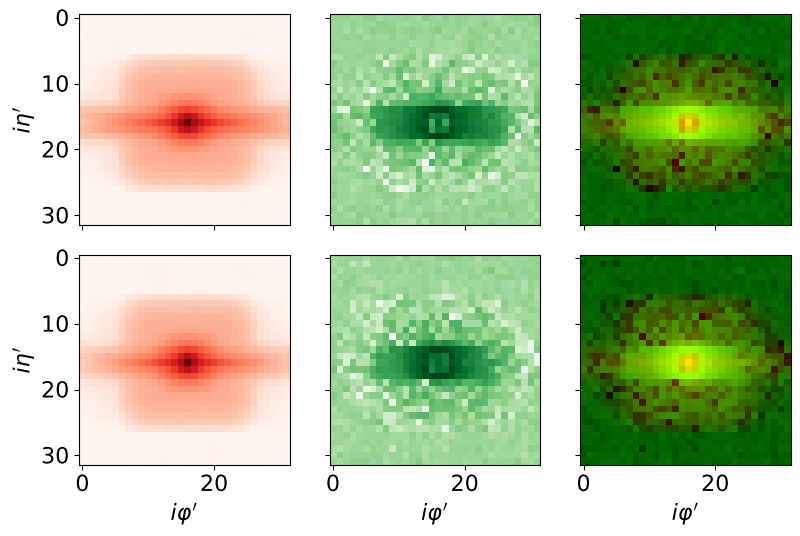
Electron-Photon
The Electron-Photon dataset is the second main dataset I've been analysing. As the Quark-Gluon dataset, the data is also derived by Andrews et al. from simulated data available on the CERN CMS Open Data Portal.
In this case, the goal is to distinguish between electron and photon showers. The dataset contains 498,000 2-channel 32x32 images, with half representing electrons and the other half representing photons. Here, only information from the CMS electromagnetic calorimeter (ECAL) is used. In particular, the first channel contains energy information (as in the Quark-Gluon dataset), and the second one contains timing information.
The following figure shows a random example of a shower for both electrons (top) and photons (bottom):
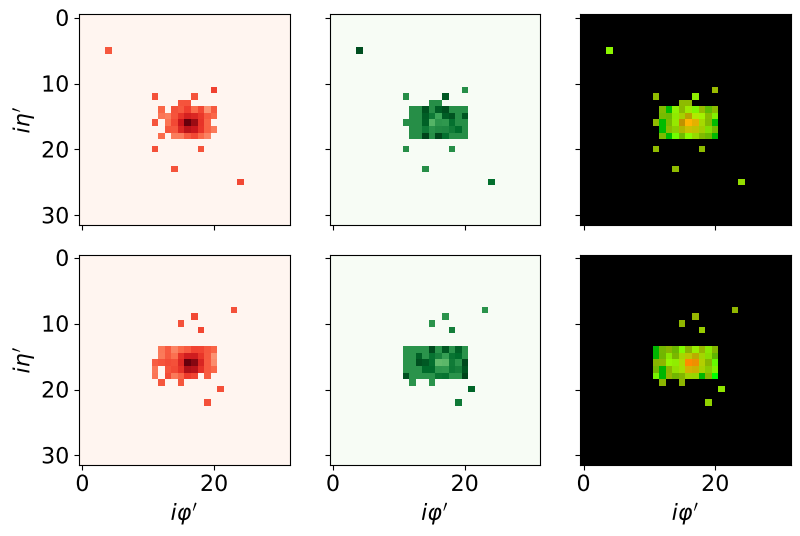
The following figure shows the average images of electrons (top) and photons (bottom) across the entire dataset:
IMDb Reviews
To test the non-Vision Transformer, that is, the model for text, I used the IMDb Reviews dataset. This dataset contains 50,000 movie reviews, which are labeled as positive or negative. The model has to predict the sentiment of the review, that is, if it's positive or negative. The dataset is split into 25,000 reviews for training and 25,000 reviews for testing. The training and testing sets are balanced, meaning that they contain an equal number of positive and negative reviews.
A random example of a positive review is the following:
if the creators of this film had made any attempt at introducing reality to the plot , it would have been just one more waste of time , money , and creative effort . fortunately , by throwing all pretense of reality to the winds , they have created a comedic marvel . who could pass up a film in which an alien pilot spends the entire film acting like jack nicholson , complete with the lakers t - shirt . do not dismiss this film as trash .
To preprocess the text, I used the BERT subword tokenizer from TensorFlow Text and padded all the sequences to the same length. Both this maximum length and also the size of the vocabulary are additional hyperparameters of the model.
Previous work
In 2021, Di Sipio et al. proposed a quantum-enhanced transformer for sentiment analysis by adapting the multi-head self-attention and feedforward layers to the quantum realm. They replaced the densely-connected linear layers used in multi-head attention with the basic entangler layers provided by PennyLane. However, the attention coefficients and the output are still calculated classically. The implementation of this work is open-source.
In parallel, Li et al. introduced Gaussian Projected Quantum Self-Attention, which they used to create a Quantum Self-Attention Neural Network for text classification. They argued that this method is more suitable for handling quantum data than the straightforward inner-product self-attention used in the work by Di Sipio et al. However, the coefficients and the output were still computed classically. The implementation of this work is also open-source.
Last year, Cherrat et al. introduced three quantum vision transformer architectures using quantum attention mechanisms. The first employs an amplitude embedding for loading matrices that they also introduce, as well as a type of layer that uses RBS (Reconfigurable Beam Splitter) gates, called Quantum Orthogonal Layers, to perform matrix-vector multiplication for calculating attention coefficients. However, the attention layer output is computed classically after obtaining the coefficients. Another proposed method extends the first one, using a quantum circuit to compute the output, making the mechanism more quantum. Lastly, another architecture with even more quantum parts, diverging more from the original transformer model, is proposed, which resembles the MLP-Mixer model by Tolstikhin et al. This third architecture combines quantum matrix data loaders, quantum orthogonal layers, and compound matrix multiplication (all these components are explained in the paper and its references). The authors of this work refused to release their implementation source code (see more details at OpenReview).
During the summer, when I had already started working on the project, a new paper was published exploring Quantum Graph Transformers by Kollias et al. However, I have not explored this work in detail yet. Other papers that might be related are "When BERT Meets Quantum Temporal Convolution Learning for Text Classification in Heterogeneous Computing" by Yang et al. (2022), and "Adapting Pre-trained Language Models for Quantum Natural Language Processing" by Li et al. (2023), although I have neither studied them thoroughly yet.
Comparison of QML frameworks
I started my project by exploring the work proposed by Di Sipio et al. and Cherrat et al., with the intention of first reproducing the results presented in these papers (note that Eyup, a fellow contributor also working on QViTs decided to focus on exploring the other proposal by Li et al.). However, the first challenge I encountered was that the models were extremely slow to train, although I was using an NVIDIA A100 GPU with 80 GB of GPU RAM running on NERSC's Perlmutter, the eighth most powerful supercomputer in the world! The paper by Di Sipio et al. also mentioned that training their model for a single epoch took over 100 hours, making it prohibitive to evaluate modifications of the model or tune the hyperparameters. In fact, if you search "pennylane slow to train" in Google, the first result is a post in the PennyLane forum by Di Sipio himself asking for help to speed up the execution. Note that, as Di Sipio, I was also using the PennyLane framework at first. However, Gopal, another fellow contributor working on QGNNs, suggested I try TensorCircuit, which claims to be much faster than PennyLane.
Before reimplementing everything with TensorCircuit, I decided to first compare both frameworks with smaller toy experiments. This way, the benchmark could be used to clearly compare both frameworks, which can be helpful for future QMLHEP contributors to avoid wasting time. Moreover, the same experiments could also be used to compare the performance of more frameworks in the future. Furthermore, I also tested the combinations of PennyLane and TensorCircuit with JAX and PyTorch (note that typically QML frameworks are used in combination with a classical deep learning framework). At first, I was using PennyLane with PyTorch, as it's the framework I'm most familiar with. However, I also tried JAX as TensorCircuit's documentation recommends it for better performance.
The results of the benchmarks were quite clear. TensorCircuit was much faster than PennyLane! Furthermore, not only was the execution faster, but the obtained AUC scores were also higher. In particular, the fastest configuration was indeed to use TensorCircuit together with JAX. More details about the benchmark and the results can be found in the directory quantum_transformers/qmlperfcomp of the code repository.
With this in mind, I decided to learn both TensorCircuit and JAX, as I had never used them before. Then, I reimplemented the code I had, and finally, I was able to execute the models with much less than 100 hours per epoch (more details on the experiments next). Note that as JAX does not provide data loading functionalities, I used TensorFlow Datasets to load the data.
Model, findings, and results
As mentioned earlier, I started my project by first trying to reimplement the proposed methods in the papers by Di Sipio et al. and by Cherrat et al.
On the one hand, after solving the performance problems, I was able to reproduce the results presented by Di Sipio et al., and not only that, but thanks to using TensorCircuit it was much, much faster!
On the other hand, I encountered challenges when attempting to reproduce the results presented by Cherrat et al. Specifically, the models failed to train due to NaN values in the gradient. Some explanations in their work seemed unclear, which may have led to potential errors in my code (my partial implementation can be found in the qvit_cerrat_et_al.ipynb notebook). Unfortunately, the authors of the paper refused to release their implementation source code, so I was not able to compare my implementation with theirs. I also contacted them to ask for help, but I did not receive any response. The concerns about reproducibility in the paper are also shared by the reviewers of the paper at OpenReview, where it was submitted to the ICLR 2023 conference and subsequently rejected due to these and other weaknesses.
I believe this situation underscores the importance of promoting open science and open source initiatives. Such transparency not only ensures the verifiability of presented results but also fosters collaborative advancements in the field. This philosophy aligns with the mission of organizations like ML4SCI and programs such as Google Summer of Code, which I am grateful to have been a part of.
Notwithstanding these issues with the paper by Cherrat et al., I was able to build upon the work by Di Sipio et al. In particular, I adapted it to the Vision Transformer architecture, as it was originally proposed for the original Transformer architecture for text processing. Furthermore, thanks to the faster implementation using TensorCircuit, I was able to experiment multiple hyperparameters and try different quantum circuits. Finally, I also explored the application of the proposed Quantum Vision Transfomer to the high-energy physics datasets, which contain hundreds of thousands of samples, many more than the dataset used in the work by Di Sipio et al., which was the IMDb Reviews datasets also described before. This made it possible to assess the scalability of the model, as well as show that it is a feasible approach to delegate some processing to quantum computers when working with the vast amounts of data that have to be processed in high-energy physics.
In the model I proposed, as in the original classical ViT, the image is split into patches, which are linearly embedded together with position embeddings. Nonetheless, the change introduced is that these patches are instead fed to the Quantum Transformer Encoder, which employs variational quantum circuits (VQCs) in the multi-head attention (MHA) and multi-layer perceptron (MLP) components. The following diagram, inspired by the ones presented in the original Transformer and Vision Transfomer papers, shows an overview of the proposed Quantum Vision Transformer model (the Q in MHA and MLP stands for quantum):
More concretely, the output of the classical multi-head attention layer is computed as:
$$ \mathrm{MultiHead}(Q, K, V) = \mathrm{Concat(head_1, ..., head_h)}W^O $$
where
$$ \mathrm{head_i} = \mathrm{Attention}(QW_i^Q, KW_i^K, VW_i^V), \\ $$
and
$$ \mathrm{Attention}(Q, K, V) = \mathrm{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$
where $W_i^Q$, $W_i^K$, $W_i^V$, and $W^O$ are parametrized matrices to compute linear projections, thus typically implemented as fully-connected layers. Here, instead, VQCs act as the classical fully-connected layers. Similarly, in the MLP component of the encoder, VQCs replace classical fully-connected layers.
In particular, the VQC configuration is as follows:
First, each feature of the vector $x=(x_0, ..., x_{n})$ is embedded into the qubits by encoding them into their rotation angles, in particular, on the X axis. Next, a layer of one-parameter single-qubit rotations acts on each wire. These parameters, $\theta = (\theta_0, ..., \theta_n)$, are learned together with the rest of the parameters of the model. Then, a ring of CNOT gates follows to entangle the qubit states. Thus, the obtained behavior is similar to a matrix multiplication. Finally, each qubit is measured, and the output is fed to the next corresponding component of the encoder.
Each multi-head attention layer uses four circuits, one for each matrix in the classical multi-head attention formulas. These circuits have a number of qubits equal to the hidden size dimension of the transformer. Likewise, the feedforward layers use one circuit, which has a number of qubits equal to the dimension of the feedforward layers.
For each dataset, I trained both a classical and a quantum vision transformer (or transformer in the case of the IMDb text dataset), with the best hyperparameters found using random hyperparameter search. I used Ray Tune to execute the search in parallel using multiple compute nodes from the Perlmutter supercomputer. The parameters were optimized with the AdamW optimizer with gradient clipping, and a learning rate scheduler that first performs a linear warmup, followed by cosine decay. The models are small so that the circuits do not require many qubits. Consequently, the simulation time is not very long, and the model could be executed on already-existing quantum hardware. Note that larger classical models can be trained to obtain even more accurate results. However, the goal here was to compare models of similar size.
The area under the ROC curve (AUC) is computed for each epoch of each model configuration on the validation set (10% of the training data). After all the epochs, the parameters from the epoch that achieves the highest validation AUC are selected, and the model is reevaluated with them on the separate hold-out test set to obtain the final test AUC. The particular hyperparameters used can be found in the notebooks in the code repository.
The obtained AUC scores for the different datasets are shown in the following table:
| Dataset | Classical | Quantum |
|---|---|---|
| MNIST Digits | 99.71% | 98.94% |
| Quark-Gluon | 79.76% | 77.62% |
| Electron-Photon | 76.50% | 77.93% |
| IMDb Reviews | 91.54% | 89.46% |
We observe that the proposed quantum transformers obtain almost the same AUC as the classical baseline, though it still lags some percentage point in most of the cases. I hypothesize that one potential reason for the slightly inferior performance of the quantum model is that it is harder for the optimizer to find good parameters within the numerically simulated VQCs. Alternatively, the proposed VQCs might lack the expressiveness required to match or exceed the performance of the classical model.
The training time per epoch is shown in the following table:
| Dataset | Classical | Quantum |
|---|---|---|
| MNIST Digits | 4.01s | 11.28s |
| Quark-Gluon | 62.91s | 1804.82s |
| Electron-Photon | 11.24s | 35.98s |
| IMDb Reviews | 3.98s | 70.18s |
The quantum models are slower to train, mainly because to train them, the quantum circuits have to be simulated, which is computationally expensive. However, the training times are still very reasonable, attaining times much lower than the 100 hours per epoch that were required by Di Sipio et al.
Finally, I also tried the effect of changing the circuit architecture to use rotations on the three X, Y, and Z axes instead of just the X axis, as well as the effect of using a different number of layers. Nonetheless, I did not observe any significant improvement in the results. All the results and details of the experiments can be found in the notebooks in the code repository.
Future work
Moving forward, several directions could be explored. First, techniques that have been shown to improve classical ViTs could also be evaluated on the QViTs, such as data augmentation with RandAugment and Mixup. Different configurations for the VQCs could also be explored, as could the usage of some techniques particular to QML such as data re-uploading to check if a quantum advantage is attained. Moreover, it could also be interesting to explore the effect of the number of samples on the performance of the models as well as their scalability to larger datasets. It would also be nice to execute the VQCs on real quantum hardware to measure the performance of the proposed QViT there as well as its robustness to quantum noise. Finally, the architecture itself could be extended by incorporating more quantum components, although it remains to be seen how this could be done without diverging too much from the original ViT architecture.
Final thoughts and acknowledgements
Participating in Google Summer of Code and contributing to ML4SCI has been a very enriching experience for me. It opened the doors to a research field I was unfamiliar with, and I'm humbled to have had the opportunity to contribute to it.
I owe a debt of gratitude to my mentors, especially Sergei Gleyzer, for their invaluable guidance. I'd also like to extend my thanks to my fellow contributors, whose ideas and assistance enriched the project further.
Moreover, a shoutout is also due to the Google Summer of Code team for orchestrating such an incredible program. Overall, I believe that GSoC is an amazing program, and the value of openness cannot be stressed enough. I sincerely appreciate Google for funding this initiative, making experiences like mine possible.
Lastly, our work was supported by the immense computational power of the United States National Energy Research Scientific Computing Center's Perlmutter supercomputer. I would also like to thank them for providing the resources and support that also contributed to completing this project.